题目内容:
设,在x=0连续,且对任何x,y∈R有f(x﹢y)=f(x)﹢f(y)
证明:(1)f在R上连续;(2)f(x)=xf(1)。
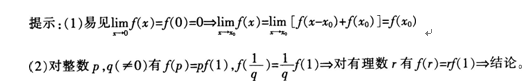
答案解析:
设,在x=0连续,且对任何x,y∈R有f(x﹢y)=f(x)﹢f(y)
证明:(1)f在R上连续;(2)f(x)=xf(1)。